مقال | نظام Bimary System: لغة الآلة 1 0 1 0
عندما تُشغّل هاتفك أو ترسل رسالة، يحدث شيء مذهل خلف الكواليس: كل حرف، كل صورة، كل صوت يتحول إلى سلسلة من (0 و1) Bimary System.
هذه ليست مجرد نظرية رياضية، بل هي اللغة الوحيدة التي تفهمها الأجهزة الإلكترونية. لكن كيف نقرأ هذه اللغة؟ وكيف تُترجم إلى أشياء ملموسة؟ إليك أمثلة عملية ستُدهشك!
التعريف البسيط : ما هو النظام الثنائي Bimary System ؟
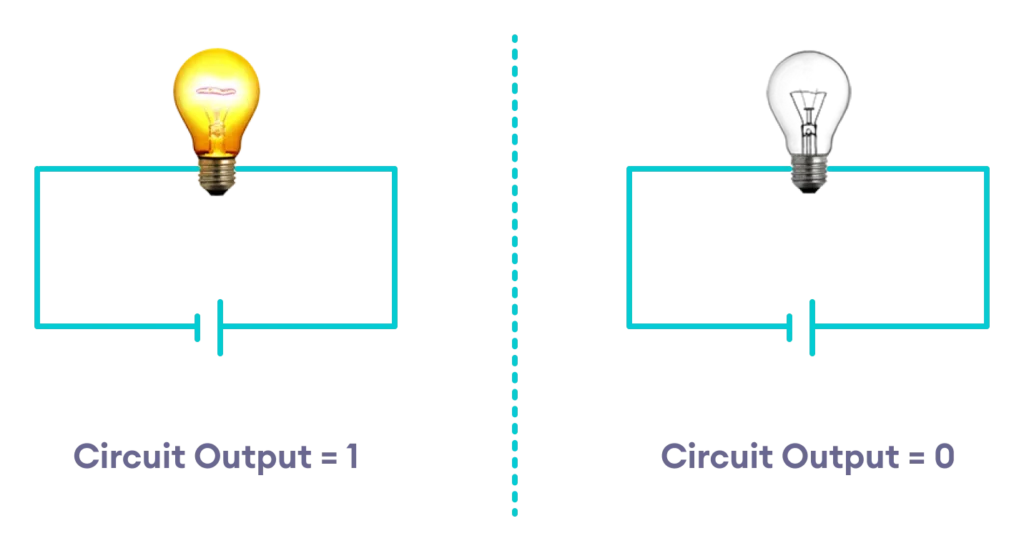
النظام الثنائي هو طريقة لتمثيل البيانات باستخدام رمزين فقط: 0 و1. يعتمد على فكرة “التشغيل” (1) و”الإيقاف” (0)، وهو أساس عمل كل الأجهزة الرقمية، من الهواتف إلى الحواسيب العملاقة.
لماذا يُسمى “ثنائي”؟
- لأنه يستخدم أساس العد 2 (على عكس النظام العشري الذي يستخدم الأساس 10).
- كل خانة تُسمى بِت (Bit)، وكل 8 بِتات تُشكل بايت (Byte).
من أين جاءت الفكرة؟ رحلة 1 : 0 عبر الزمن
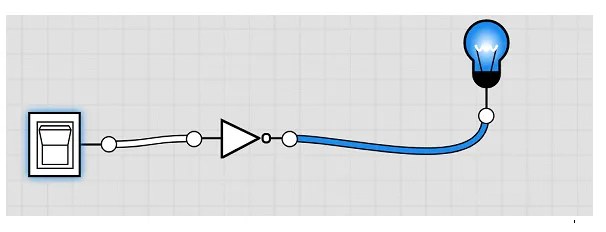
قبل أن تُصبح “0 و1” لغة الحواسيب، كانت رحلة طويلة من الفلسفة والرياضيات:
- في الهند القديمة (القرن الثالث): اكتشف الفيلسوف بينجالا أول نظام ثنائي لوصف الإيقاعات الشعرية، لكنه بقي حبيس الكتب.
- عام 1703: عالم الرياضيات الألماني غوتفريد لايبنتز أعاد اكتشاف النظام ووصفه بأنه “انعكاس لخلق الكون من العدم (0) والوجود (1)”، حتى أنه أرسل شرحاً للإمبراطور الصيني على أمل أن يرى فيه رمزاً روحانياً! “طبعاً نحن لأ نؤمن بهذا الخرفات“
- القرن العشرين: جاءت الثورة الرقمية لتحول النظرية إلى واقع. اكتشف العلماء أن الترانزستورات (التي تعمل “تشغيل” أو “إيقاف“) هي الوسيلة المثلى لتمثيل هذه الأرقام.
كيف يعمل هذا النظام ؟ بعض الامثلة على ذلك

تخيل أنك تمتلك عدد من المصابيح الكهربائية:
- المصباح المطفأ = 0 (لا تيار).
- المصباح المضاء = 1 (تيار كامل).
مثال على تحويل الرقم 1990 من النظام العشري إلى الثنائي:
- اقسم الرقم على 2، ثم اكتب الباقي (0 أو 1).
- كرر العملية مع ناتج القسمة حتى يصبح الناتج 0.
- اقرأ البواقي من الأسفل إلى الأعلى لتحصل على الرقم الثنائي.
| الخطوة | العملية الحسابية | الناتج | الباقي (0 أو 1) | التفسير |
|---|---|---|---|---|
| 1 | 1990 ÷ 2 | 995 | 0 | لأن 1990 عدد زوجي |
| 2 | 995 ÷ 2 | 497 | 1 | لأن 995 عدد فردي |
| 3 | 497 ÷ 2 | 248 | 1 | لأن 497 عدد فردي |
| 4 | 248 ÷ 2 | 124 | 0 | لأن 248 عدد زوجي |
| 5 | 124 ÷ 2 | 62 | 0 | لأن 124 عدد زوجي |
| 6 | 62 ÷ 2 | 31 | 0 | لأن 62 عدد زوجي |
| 7 | 31 ÷ 2 | 15 | 1 | لأن 31 عدد فردي |
| 8 | 15 ÷ 2 | 7 | 1 | لأن 15 عدد فردي |
| 9 | 7 ÷ 2 | 3 | 1 | لأن 7 عدد فردي |
| 10 | 3 ÷ 2 | 1 | 1 | لأن 3 عدد فردي |
| 11 | 1 ÷ 2 | 0 | 1 | لأن 1 عدد فردي |
الخطوة الثانية: اكتب البواقي من الأسفل إلى الأعلى
- البواقي من الخطوة 11 إلى الخطوة 1 هي:
1 1 1 1 1 0 0 0 1 1 0 - إذن، الرقم الثنائي لـ 1990 هو:
11111000110
كيف تتأكد أن النتيجة صحيحة؟
طريقة التحقق:
- اكتب الرقم الثنائي:
1 1 1 1 1 0 0 0 1 1 0 - ابدأ من اليمين إلى اليسار، واجمع قوى الرقم 2 لكل خانة فيها 1:
- الجمع القيم : 1024+512+256+128+64+4+2=1990
4. مثال آخر لتحويل رقم صغير (للفهم):
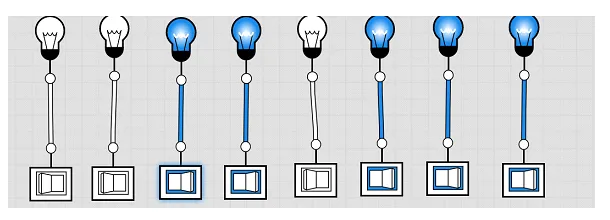
حول الرقم 10 إلى ثنائي:
| الخطوة | العملية | الناتج | الباقي | التفسير |
|---|---|---|---|---|
| 1 | 10 ÷ 2 = 5 | 5 | 0 | زوجي |
| 2 | 5 ÷ 2 = 2 | 2 | 1 | فردي |
| 3 | 2 ÷ 2 = 1 | 1 | 0 | زوجي |
| 4 | 1 ÷ 2 = 0 | 0 | 1 | فردي |
- البواقي من الأسفل إلى الأعلى: 1 0 1 0 → 1010
هذا بالضبط ما يحدث داخل معالج الكمبيوتر، لكن بدلًا من المصابيح، هناك مليارات الترانزستورات التي تضيء وتنطفئ بسرعة تريليونات المرات في الثانية!
وبالتالي نستطيع ان نستنتج ان اجهزة الكمبيوتر لا تتعامل مع لغتنا ابداً ، ولكن تتعامل معنا او نتعامل معها برقمين فقط وهما 1 0
كيف يتم تحويل الحروف : التحويل من حروف الى 1 0
يتم تحويل جميع الحروف والرموز مثل “@ او ! او *” الى الارقام 1 0 عبر مايسمى بي اكواد أسكي كود.
ما هو أسكي كود؟

ASCII ببساطة هو اختصار لـ “American Standard Code for Information Interchange” ويشير إلى مجموعة محددة من الرموز المستخدمة لتمثيل الحروف والأرقام والرموز الأخرى في الحواسيب وأنظمة الاتصالات.
تم تطوير ASCII في الأصل في عام 1963 كمعيار لتبادل البيانات بين أجهزة الكمبيوتر المختلفة والشبكات.
وتتضمن مجموعة ASCII الأصلية 128 رمزًا، حيث يمثل كل حرف بواحد من هذه الرموز، وتتضمن الرموز الأساسية الأبجدية اللاتينية الكبيرة والصغيرة، والأرقام من 0 إلى 9، ورموز ترقيم ورموز تحكم مثل المسافة والترقيم والعلامات القوسية والأقواس.
ومع مرور الوقت، تطورت مجموعة ASCII لتشمل مجموعة أوسع من الرموز تسمح بتمثيل الأحرف والرموز الإضافية بما في ذلك الحروف غير اللاتينية والرموز الخاصة. يتكون ASCII الموسع من 8 بت، مما يعني وجود 256 رمزًا ممكنًا.
وحاليًا تُستخدم ASCII بشكل واسع في البرمجة وعند نقل البيانات بين الأجهزة المختلفة، حيث يمكن تمثيل النصوص والرموز باستخدام تلك المجموعة المحددة من الأرقام والحروف.
والغرض هو توحيد تلك التمثيلات في جميع أنحاء الأنظمة التي تدعم ASCII لضمان التوافق وتبادل البيانات بسهولة.
مثال للتوضيح:
- حرف “A” بالأحرف الكبيرة: يتم تمثيله بالرقم 65 في ASCII.
- حرف “a” بالأحرف الصغيرة: يتم تمثيله بالرقم 97 في ASCII.
- الرقم “5“: يتم تمثيله بالرقم 53 في ASCII.
- الرمز “$“: يتم تمثيله بالرقم 36 في ASCII.
- الرمز التحكم للمسافة الفارغة: يتم تمثيله بالرقم 32 في ASCII.
جدول أسكي مصغّر:
| الحرف | الرقم (عشري) | التمثيل الثنائي |
|---|---|---|
| A | 65 | 01000001 |
| a | 97 | 01100001 |
| $ | 36 | 00100100 |
| 5 | 53 | 00110101 |
قوم باخذ هذه الارقام على سبيل المثال رقم 65 والذي يرمز الى حرف “A” وقوم بتحويله الى النظام الثنائي وسوف تجد الناتج 01000001.
3. التمثيل الثنائي لـ 65 بناءً على التحليل الصحيح:
| القيمة | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| البِت | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
- الرقم الثنائي: 1000001
- التحقق: 64+0+0+0+0+0+1=65 ✅
لماذا لا نستخدم انظمة اخرى ؟ جواب مُدهش!

لو استخدمت الحواسيب على سبيل المثال النظام العشري، لاحتاج كل ترانزستور إلى 10 حالات مختلفة (من 0 إلى 9)، وهذا مستحيل عمليًا بسبب:
- البطء الشديد: تحديد الحالة بدقة بين 10 مستويات يستغرق وقتًا أطول.
- الأخطاء الكارثية: أي تدخل كهربائي بسيط سيُغيّر القيمة (مثل تحويل 5 إلى 6).
- الحجم الضخم: حجم المعالج سيزيد عشرات المرات!
النظام الثنائي في حياتك اليومية: أمثلة لا تُصدق!

1. صورة السيلفي التي تشاركها:
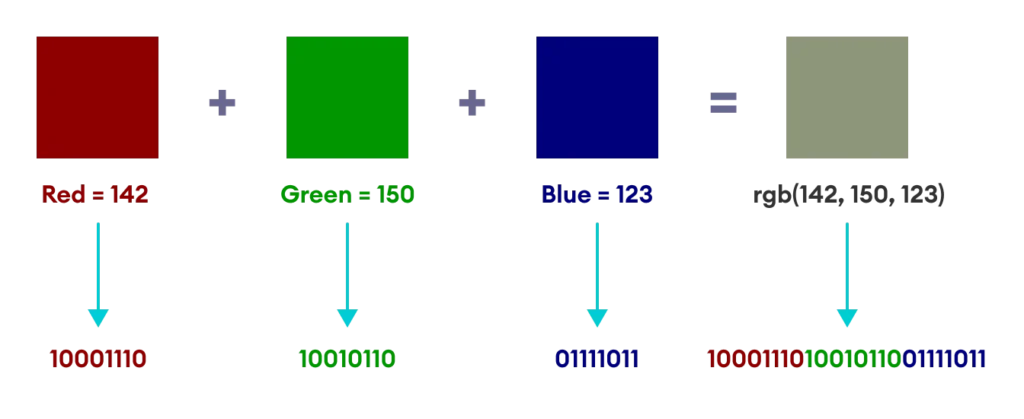
- تُقسّم إلى ملايين البكسلات.
- كل بكسل يُخزَّن كـ 3 قيم ثنائية (للأحمر، الأخضر، الأزرق).
- مثال: اللون الأرجواني = أحمر: 11111111، أزرق: 11111111، أخضر: 00000000.
2. الأغنية التي تستمع إليها:
- تُحوّل الموجات الصوتية إلى سلسلة من 0 و1 عبر عملية تسمى التنميط الرقمي (Digital Sampling).
3. كلمة المرور التي تحمي حسابك:
- مثل “P@ssw0rd” تُخزَّن كـ 01010000 01000000 01110011 01110011 01110111 00110000 01110010 01100100.
مستقبل الثنائي: هل سيحل مكانه شيء آخر؟
مع تطور تقنيات مثل الحوسبة الكمية، التي تستخدم الكيوبتات (التي يمكن أن تكون 0 و1 في نفس الوقت)، قد يتغير المشهد. لكن الخبراء يتوقعون:
- الثنائي سيظل الأساس: لأنه الأبسط والأكثر استقرارًا.
- التحديات: تصميم أنظمة تدعم أكثر من حالتين دون أخطاء ما زال صعبًا.
خاتمة: الأصفار والوحدات… ليست مجرد أرقام، بل هي ذاكرة البشرية!
النظام الثنائي هو الدليل على أن البساطة قد تُنتج أعظم التعقيدات. كل ضغطة زر، كل تغريدة، كل اكتشاف علمي… يُختزل إلى سلسلة من 0 و1 تختبئ في زوايا الذاكرة الرقمية للعالم.
جرب بنفسك:
- اكتب اسمك في محول النصوص إلى ثنائي.
- شاهده يتحول إلى شفرة سرية هذه هي قوة النظام الثنائي!
